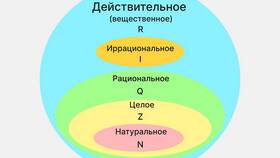
Сумма двух векторов - это новый вектор, получаемый в результате операции сложения исходных векторов. Векторное сложение подчиняется определенным математическим правилам и имеет четкую геометрическую интерпретацию.
Содержание
Основные способы сложения векторов
| Метод | Описание |
| Правило треугольника | Векторы откладываются последовательно друг за другом |
| Правило параллелограмма | Векторы откладываются из одной начальной точки |
| Аналитический метод | Сложение соответствующих координат векторов |
Геометрическое сложение векторов
Правило треугольника
- Отложить первый вектор a от произвольной точки
- От конца вектора a отложить вектор b
- Вектор, соединяющий начало первого и конец второго вектора, будет суммой a + b
Правило параллелограмма
- Отложить оба вектора от одной точки
- Достроить параллелограмм на этих векторах
- Диагональ параллелограмма, исходящая из общей точки, будет суммой векторов
Аналитический метод сложения
Для векторов, заданных координатами в декартовой системе:
| Тип векторов | Формула сложения |
| На плоскости | a + b = (ax + bx; ay + by) |
| В пространстве | a + b = (ax + bx; ay + by; az + bz) |
Пример вычисления
Для векторов a = (2; 5) и b = (3; -1):
- a + b = (2 + 3; 5 + (-1)) = (5; 4)
Свойства суммы векторов
- Коммутативность: a + b = b + a
- Ассоциативность: (a + b) + c = a + (b + c)
- Существование нулевого вектора: a + 0 = a
- Существование противоположного вектора: a + (-a) = 0
Применение суммы векторов
| Область | Пример использования |
| Физика | Сложение сил, скоростей, ускорений |
| Компьютерная графика | Перемещение объектов, расчет освещения |
| Навигация | Расчет результирующего движения |
Физический пример
Если на тело действуют две силы F1 = 3 Н и F2 = 4 Н под прямым углом:
- Результирующая сила F = √(3² + 4²) = 5 Н
Сумма векторов является фундаментальной операцией в векторной алгебре, имеющей как теоретическое значение, так и практическое применение в различных областях науки и техники.